Receiver Operating Characteristic based on Power Lindley Distribution

ROC curve analysis is performed assuming samples are from the Power Lindley distribution. Specificity, sensitivity, area under the curve and ROC curve are provided.

Usage

dPLD(x, alpha, beta)

pPLD(x, alpha, beta)

qPLD(p, alpha, beta)

rPLD(n, alpha, beta)

r.pl_auc(
  x,
  y,
  init_param = c(alpha1 = 1, beta1 = 1, alpha2 = 1, beta2 = 1),
  true_param = c(alpha1 = 1, beta1 = 1, alpha2 = 1, beta2 = 1),
  method = c("MLE", "AD", "CvM", "LSE", "WLSE", "TRUE")
)

r.pl_index(
  x,
  y,
  init_param = c(alpha1 = 1, beta1 = 1, alpha2 = 1, beta2 = 1),
  init_index = 1,
  true_param = c(alpha1 = 1, beta1 = 1, alpha2 = 1, beta2 = 1),
  method = c("MLE", "AD", "CvM", "LSE", "WLSE", "TRUE")
)

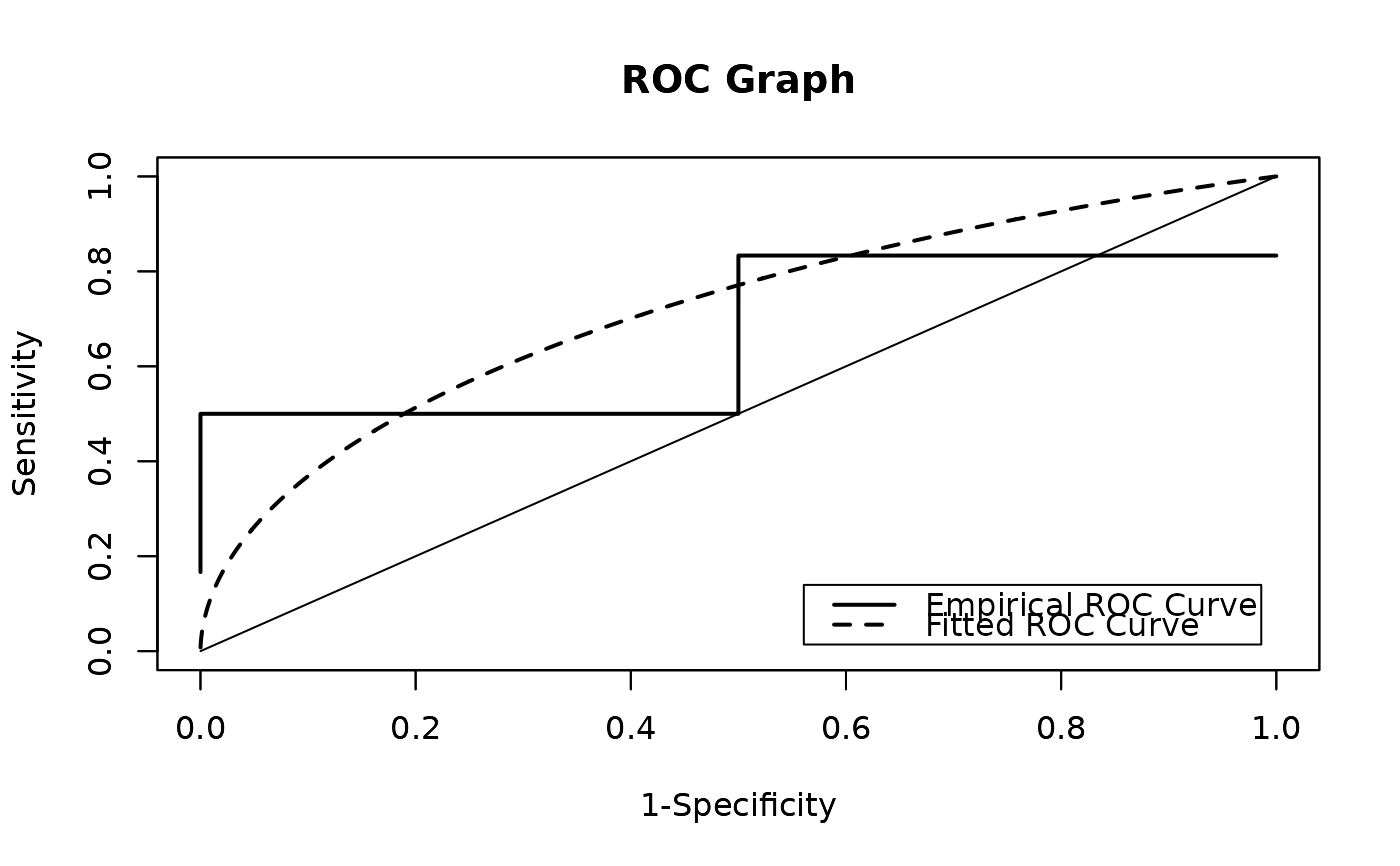
r.pl_graph(
  x,
  y,
  init_param = c(alpha1 = 1, beta1 = 1, alpha2 = 1, beta2 = 1),
  true_param = c(alpha1 = 1, beta1 = 1, alpha2 = 1, beta2 = 1),
  empirical = TRUE,
  method = c("MLE", "AD", "CvM", "LSE", "WLSE", "TRUE")
)

Arguments

x, y

vector of quantiles.

alpha

shape parameter.

beta

scale parameter.

p

vector of probabilities.

n

number of observations. If length(n) > 1, the length is taken to be the number required.

init_param

initial paremeter values for the estimation method.

true_param

true parameter values.

method

estimation method. The default value for the method is "MLE".

init_index

initial index value for the optimization calculation.

empirical

empirical must be TRUE or FALSE.

alpha1

shape parameter of distribution of first sample.

beta1

scale parameter of distribution of first sample.

alpha2

shape parameter of distribution of second sample.

beta2

scale parameter of distribution of second sample.

Value

dPLD gives the probability density function of Power Lindley Distribution.

pPLD gives the cumulative density function of Power Lindley Distribution.

qPLD gives the quantile function of Power Lindley Distribution.

rPLD gives random numbers from Power Lindley Distribution.

r.pl_auc gives the Area Under the Curve (AUC) when the data conforms to the Power Lindley Distribution.

r.pl_index gives index values when the data conforms to the Power Lindley Distribution.

r.pl_graph gives the ROC curve when the data conforms to the Power Lindley Distribution.

Details

The probability density function (PDF) and cumulative distribution function (CDF) are as follows: $$f\left( x;\boldsymbol{\theta }\right) =\frac{\alpha \beta ^{2}}{ \beta +1}\left( 1+x^{\alpha} \right) x^{\alpha -1}\exp \left( -\beta x^{\alpha }\right)$$ $$=zg_{1}\left( t\right) +\left( 1-z\right) g_{2}\left( t\right),$$

$$F\left( x;\boldsymbol{\theta }\right) =P\left( X\leq x\right) =1- \left( 1+zx^{\alpha } \right) \exp \left( -\beta x^{\alpha }\right),$$ and quantile function is given by $$Q\left( u;\boldsymbol{\theta }\right) =F^{-1}\left( u; \boldsymbol{\theta }\right) =\left\{ -\frac{W\left( \left( 1+\beta \right) \left( -1+u\right) \exp \left( -\left( 1+\beta \right) \right) \right) +1+\beta } {\beta }\right\} ^{\frac{1}{\alpha }},$$ where $$z =\frac{\beta }{\beta +1},$$ $$g_{1}\left( x\right) =\alpha \beta x^{\alpha -1}\exp \left( -\beta x^{\alpha }\right),$$ $$g_{2}\left( x\right) =\alpha \beta ^{2}x^{2\alpha -1}\exp \left(-\beta x^{\alpha }\right),$$ \(\boldsymbol{\theta =}\left( \alpha ,\beta \right) \), \(0<u<1\), \(\alpha>0\) is a shape parameter, \(\beta>0\) is a scale parameter and W(•) is Lambert W function.

Additionally, the estimation methods Anderson-Darling "AD", Cramér-von Mises "CvM", least squares "LS" and weighted least squares "WLS" as well as the "TRUE" option for the true value, are available. Please note that the default value for the method parameter is maximum likelihood "ML" estimation.

The cut-off point values corresponding to Youden's J index (J), the criterion closest to (0, 1) (ER), the concordance probability method (CZ), and the newly proposed Ertan-Coskun index (EC) are provided.

References

Akgenç, E., and Kuş, C., 2023, ROC Curve Analysis for the Measurements Distributed Power-Lindley Distribution, 2nd International E-Conference On Mathematical And Statistical Sciences: A Selçuk Meeting (ICOMSS-2023), Konya, 25.

Attwood, K., Hou, S., and Hutson, A., 2022, Application of the skew exponential power distribution to ROC curves, Journal of Applied Statistics, 1-16.

Ghitany M., Al-Mutairi D. K., Balakrishnan N., and Al-Enezi L., 2013, Power lindley distribution and associated inference, Computational Statistics & Data Analysis, 64,20–33.

Liu, X., 2012, Classification accuracy and cut point selection, Statistics in medicine, 31(23), 2676-2686.

Nahm, F. S., 2022, Receiver operating characteristic curve: overview and practical use for clinicians, Korean journal of anesthesiology, 75(1), 25-36.

Perkins, N. J., and Schisterman, E. F., 2006, The inconsistency of “optimal” cutpoints obtained using two criteria based on the receiver operating characteristic curve, American journal of epidemiology, 163(7), 670-675.

Pundir, S. and Amala, R., 2014, Evaluation of area under the constant shape bi-weibull roc curve, Journal of Modern Applied Statistical Methods, 13(1),1-20.

Youden, W. J., 1950, Index for rating diagnostic tests, Cancer, 3(1), 32-35.

Examples

dPLD(c(1,2,3,4,5,200),alpha=3,beta=2)
#> [1]  1.082682e+00  1.620507e-05  3.560890e-21  1.070039e-52 3.363180e-105
#> [6]  0.000000e+00
pPLD(c(.5,1,2,3,4),alpha=3,beta=2)
#> [1] 0.1562992 0.7744412 0.9999993 1.0000000 1.0000000
qPLD(c(.9971,0.5,0.3),alpha=3,beta=2)
#> [1] 1.5220612 0.7868721 0.6362570
rPLD(10,alpha=3,beta=2)
#>  [1] 0.3968803 1.0600360 0.8598761 0.5010362 0.1772106 0.7626490 0.7852732
#>  [8] 0.6277847 0.9632404 0.9982308
r.pl_auc(x=c(1,2,2,3,1),y=c(1,3,2,4,2,3),
true_param=c(alpha1=1,beta1=1,alpha2=1,beta2=1),method=c("TRUE"))
#> [1] 0.5
r.pl_index(x=c(1,2,2,3,1),y=c(1,3,2,4,2,3),init_param=c(1,1,1,1),
init_index=1,method=c("MLE"))
#>    Cut-off Point Sensitivity Specificity 1-Specificity
#> J       2.257651   0.5843951   0.7345488     0.2654512
#> ER      2.128638   0.6365278   0.6790223     0.3209777
#> CZ      2.155423   0.6258267   0.6909883     0.3090117
#> EC      2.049502   0.6676484   0.6424604     0.3575396
x=c(1,2,2,3,1)
y=c(1,3,2,4,2,3)
r.pl_graph(x,y,init_param=c(1,1,1,1),
empirical=TRUE,method=c("MLE"))